Question types

Source: vignettes/question_types.Rmd

Exam documents are basically a collection of questions. Questions are added to an exam by calling any of the *_question() functions from an R code chunk in the exam document. Currently examinr supports two basic kinds of questions: multiple-choice questions and “text” questions. Text questions encompass any kind of question requiring the learner to enter a value in a text box, including numeric answers.

Questions are by default identified by the label of the R code chunk in which they are defined. If you want to define multiple questions in one code chunk, you must use the id argument to set a unique id (unique within the exam document).

Multiple-choice questions

Multiple-choice and multiple-response questions are added via mc_question(). The question is by default multiple-response (argument checkbox=TRUE) and answer options are displayed with check-boxes, allowing the learner to select any number of answer options.

The following R code produces a simple MC question displayed below

#! context="render"
mc_question(
  title = "If $X$ follows a standard Normal distribution, what statements are true?",
  points = 2,
  answer(r"($\Pr(X = 0) = 0$)", correct = TRUE),
  answer(r"($\Pr(X > 0) > 0$)", correct = TRUE),
  answer(r"($X$ follows a _continuous_ distribution.)", correct = TRUE),
  answer(r"($X$ follows a _discrete_ distribution.)"),
  answer(r"($\Pr(X = 0) > 0$)"),
  answer(r"($\Pr(X < 0) < 0$)"),
  answer(r"($\Pr(X > 0) = 0.25$)"),
  answer(r"($\Pr(-0.5 \leq X < 0.5) = 0.5$)"))
Multiple choice question.

Multiple choice question.

By default, mc_question() will randomly select 5 answer options from the pool of supplied answer options. At least one correct answer option is always displayed. If you would rather want to restrict learners to select only a single option, you can set checkbox=FALSE. In this case exactly one answer option will be displayed.

Answer options are added by supplying mc_question() with an arbitrary number (at least one) of unnamed objects created with answer(). An answer option is a label (the text shown to the learner) and some metadata. Both the question title and answer labels may contain commonmark markdown and LaTeX formulas (within $ delimiters). For simple answer options, as in the example above, correct may be simply a constant (TRUE or FALSE). For more complex scenarios you can also supply an expression which will be evaluated at run-time in the environment created by the data provider (explained in detail in the companion vignette on randomization). The expression must yield either TRUE or FALSE depending on the randomized values for the attempt.

Consider an example where the learner is asked to decide whether a certain test rejects the null hypothesis in favor of the alternative. Assume the data provider randomly draws the value of the test statistic (test_stat) and the significance level (sign_level), and also returns the critical value (crit_value). The MC question can be written as:

#! context="render"
mc_question(title = "Does the test reject the null at a significance level of `r significance_level`?",
            answer("Yes", correct = abs(test_stat) >= crit_value),
            answer("No", correct = abs(test_stat) < crit_value))

Changing the number of displayed answer options

The number of answer options shown at any time is determined by the argument nr_answers, which can either be a single number or a vector of two numbers.

If a single number, nr_answers determines how many answer options in total will be shown. The number of shown correct answer options is either exactly 1 (if checkbox=FALSE) or varies between 1 and nr_answers (if checkbox=TRUE).

If nr_answers is a vector of two numbers, the first number determines the number of correct answer options to display and the second number determines the number of incorrect answer options to display.

Important: You must ensure to provide enough correct and incorrect answer options to satisfy the requested number of answer options. Since correctness is only determined at run-time, examinr cannot warn you at the time of knitting if there will be enough correct/incorrect answer options available. In particular, you must ensure that at least one answer option is correct.

Grading

Multiple-choice questions are automatically graded upon submission of the section. The score on a question (out of the total points) is determined by the weight of the selected answer options.

The argument answer(weight=) is a numeric vector of two elements: the first element is the weight applied if the answer option is incorrect and the second element is the weight applied if the answer option is correct. If correct is a constant (and known when knitting), weight can also be a single number. In this case weight = w is equivalent to weight = c(0, w) if correct=TRUE or to weight = c(w, 1) if correct=FALSE.

Weights for correct answer options are standardized, such that the sum of all shown, correct answer options is 1. Weights for incorrect answer options are not standardized and interpreted as a proportion of the total points available. For example, a weight of weight = c(-0.5, 1) for an incorrect answer option would reduce the score by 50% of the total points available for the question.

The total score \(p\) is computed as

\[ p = t \times \left(\frac{ \sum_{i \in C} w_{i 2} s_i } { \sum_{i \in C} w_{i 2} } + \sum_{i \in I} w_{i 1} \right). \] where

  • \(t\) is the total number of points available for the question,
  • \(C\) and \(I\) are the set of correct and incorrect answer options, respectively,
  • \(w_{i 1}\) and \(w_{i 2}\) are the two weight values associated with the \(i\)-th answer option,
  • \(s_i\) is 1 if the learner selected answer option \(i\) and 0 otherwise.

By default a learner cannot get a negative score on a question, but this can be changed via argument mc_question(min_points=). If you would set min_points=-0.5, for example, a learner may be penalized with up to -0.5 points.

Considering the example from above (but ignoring randomization)

#! context="render"
mc_question(
  title = "If $X$ follows a standard Normal distribution, what statements are true?",
  points = 2, nr_answers = 8, random_answer_order = FALSE,
  answer(r"($\Pr(X = 0) = 0$)", correct = TRUE, weight = c(0, 2)),
  answer(r"($\Pr(X > 0) > 0$)", correct = TRUE, weight = 2),
  answer(r"($X$ follows a _continuous_ distribution.)", correct = TRUE, weight = 1),
  answer(r"($X$ follows a _discrete_ distribution.)", weight = -0.1),
  answer(r"($\Pr(X = 0) > 0$)", weight = -0.1),
  answer(r"($\Pr(X < 0) < 0$)", weight = -0.1),
  answer(r"($\Pr(X > 0) = 0.25$)", weight = 0),
  answer(r"($\Pr(-0.5 \leq X < 0.5) = 0.5$)", weight = 0))

The second answer option is worth twice as much as the other correct answer options. Selecting some of the incorrect answer options will be penalized by 10% of the total points available (i.e., by -0.2 points). This is also shown on the feedback page (for 3 different response patterns):

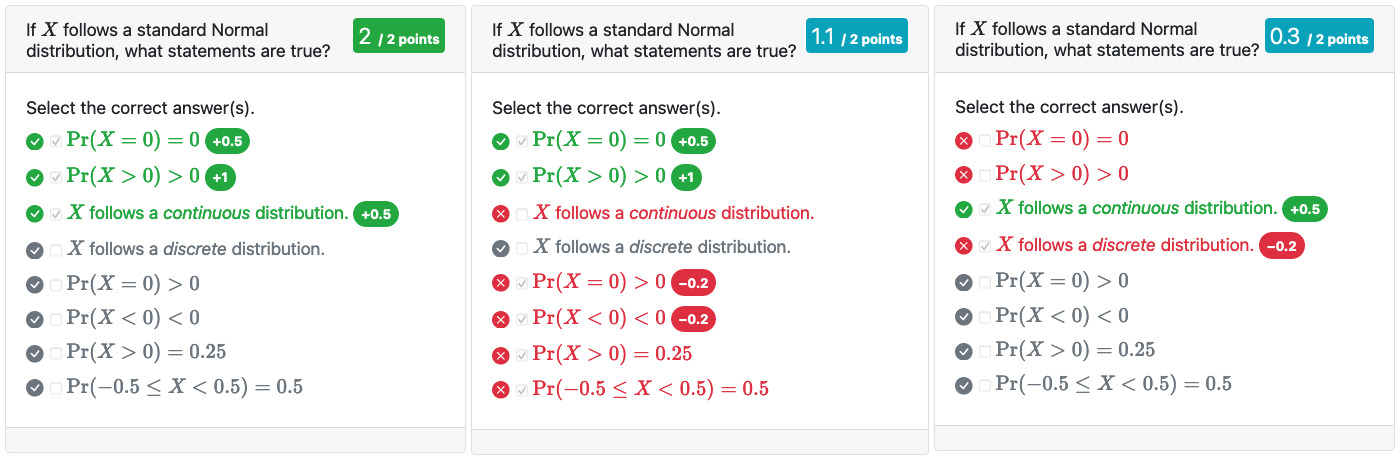
Scores for different combinations of responses.

Scores for different combinations of responses.

Changing randomization

By default mc_question() randomly selects from the pool of supplied answer options and also randomizes the order of the answer options. You can disable the shuffling by setting the argument mc_question(random_answer_order=) to FALSE. If you want an answer option to be always displayed, you can set the argument answer(always_show=) to TRUE.

Text questions

The second question type supported by examinr are text questions, created via text_question(). Currently, text questions accept either numeric answers (type="numeric"), single-line text answers (type="text"), or multi-line text answers (type="textarea").

Grading

You can supply the solution to a text question via the solution expression. The expression is evaluated at run-time and hence has access to all objects created by the data provider. The expression must yield a character string (or it will be forcefully cast to one) and can include commonmark markdown and math notation.

Moreover, numeric answers are auto-graded if the solution expression either yields (a) a numeric value or (b) a character value with numeric attribute answer. This number is compared with the learner’s answer using the function given in text_question(comp=). The comparison function must take arguments input, the value input by the learner, and answer, the correct numeric value as given by the solution expression. The comparison function can assume that input is a single number and no validation of the learner input is necessary.

The examinr package ships with 3 default comparison functions:

  • comp_abs(tol), checks if the absolute difference between the learner’s input and the correct answer is less or equal than tol (equivalent to abs(input - answer) <= tol).
  • comp_rel(tol), checks if the relative difference between the learner’s input and the correct answer is less or equal than tol (equivalent to abs(input / answer - 1) <= tol).
  • comp_digits(digits, pm), which is the default, compares the learner’s input and the correct answer rounded to digits digits significant digits after the decimal point. This allows for small discrepancies in the last digits requested from the learner. If the absolute value of the correct answer is greater than 1, the comparison is equal to abs(input - answer) < pm * 10^-digits, and hence the same as comp_abs(pm * 10^-digits). If the absolute value of the correct answer is less than 1, the comparison is equal to 10^s * abs(input - answer) < pm * 10^-digits, where s is such that abs(10^s * answer) is less than 1 and the first digit after the decimal mark is non-zero (i.e., shifting the decimal point to the right just before the first non-zero digit). Consider for example, comp_digits(digits=3, pm=1) is used to compare the learner’s input against a correct answer of 0.0000652412, anything between 0.0000651412 and 0.0000653412 would be accepted.

Mandatory questions

You can make questions mandatory by setting the argument mandatory to TRUE. Learners cannot submit the answers unless they answer the mandatory questions. For MC questions, the learner needs to select (at least) one option, and for text questions any non-empty response is accepted.