Compute (Adaptive) Elastic Net S-Estimates of Regression

Compute elastic net S-estimates (PENSE estimates) along a grid of penalization levels with optional penalty loadings for adaptive elastic net.

Usage

pense(
  x,
  y,
  alpha,
  nlambda = 50,
  nlambda_enpy = 10,
  lambda,
  lambda_min_ratio,
  enpy_lambda,
  penalty_loadings,
  intercept = TRUE,
  bdp = 0.25,
  cc,
  add_zero_based = TRUE,
  enpy_specific = FALSE,
  other_starts,
  carry_forward = TRUE,
  eps = 1e-06,
  explore_solutions = 0,
  explore_tol = 0.1,
  explore_it = 5,
  max_solutions = 5,
  comparison_tol = sqrt(eps),
  sparse = FALSE,
  ncores = 1,
  standardize = TRUE,
  algorithm_opts = mm_algorithm_options(),
  mscale_opts = mscale_algorithm_options(),
  enpy_opts = enpy_options(),
  cv_k = deprecated(),
  cv_objective = deprecated(),
  ...
)

Arguments

x: n by p matrix of numeric predictors.
y: vector of response values of length n. For binary classification, y should be a factor with 2 levels.
alpha: elastic net penalty mixing parameter with \(0 \le \alpha \le 1\). alpha = 1 is the LASSO penalty, and alpha = 0 the Ridge penalty. Can be a vector of several values, but alpha = 0 cannot be mixed with other values.
nlambda: number of penalization levels.
nlambda_enpy: number of penalization levels where the EN-PY initial estimate is computed.
lambda: optional user-supplied sequence of penalization levels. If given and not NULL, nlambda and lambda_min_ratio are ignored.
lambda_min_ratio: Smallest value of the penalization level as a fraction of the largest level (i.e., the smallest value for which all coefficients are zero). The default depends on the sample size relative to the number of variables and alpha. If more observations than variables are available, the default is 1e-3 * alpha, otherwise 1e-2 * alpha.
enpy_lambda: optional user-supplied sequence of penalization levels at which EN-PY initial estimates are computed. If given and not NULL, nlambda_enpy is ignored.
penalty_loadings: a vector of positive penalty loadings (a.k.a. weights) for different penalization of each coefficient. Only allowed for alpha > 0.
intercept: include an intercept in the model.
bdp: desired breakdown point of the estimator, between 0.05 and 0.5. The actual breakdown point may be slightly larger/smaller to avoid instabilities of the S-loss.
cc: tuning constant for the S-estimator. Default is chosen based on the breakdown point bdp. This affects the estimated coefficients only if standardize=TRUE. Otherwise only the estimated scale of the residuals would be affected.
add_zero_based: also consider the 0-based regularization path. See details for a description.
enpy_specific: use the EN-PY initial estimates only at the penalization level they are computed for. See details for a description.
other_starts: a list of other staring points, created by starting_point(). If the output of enpy_initial_estimates() is given, the starting points will be shared among all penalization levels. Note that if a the starting point is specific to a penalization level, this penalization level is added to the grid of penalization levels (either the manually specified grid in lambda or the automatically generated grid of size nlambda). If standardize = TRUE, the starting points are also scaled.
carry_forward: carry the best solutions forward to the next penalty level.
eps: numerical tolerance.
explore_solutions: number of solutions to keep after the exploration step. The best explore_solutions are then iterated to full numerical tolerance eps. If 0, all non-duplicated solutions are kept.
explore_tol, explore_it: numerical tolerance and maximum number of iterations for exploring possible solutions. The tolerance should be (much) looser than eps to be useful, and the number of iterations should also be much smaller than the maximum number of iterations given via algorithm_opts. explore_tol is also used to determine if two solutions are equal in the exploration stage.
max_solutions: retain only up to max_solutions unique solutions per penalization level.
comparison_tol: numeric tolerance to determine if two solutions are equal. The comparison is first done on the absolute difference in the value of the objective function at the solution. If this is less than comparison_tol, two solutions are deemed equal if the squared difference of the intercepts is less than comparison_tol and the squared \(L_2\) norm of the difference vector is less than comparison_tol.
sparse: use sparse coefficient vectors.
ncores: number of CPU cores to use in parallel. By default, only one CPU core is used. Not supported on all platforms, in which case a warning is given.
standardize: logical flag to standardize the x variables prior to fitting the PENSE estimates. Coefficients are always returned on the original scale. This can fail for variables with a large proportion of a single value (e.g., zero-inflated data). In this case, either compute with standardize = FALSE or standardize the data manually.
algorithm_opts: options for the MM algorithm to compute the estimates. See mm_algorithm_options() for details.
mscale_opts: options for the M-scale estimation. See mscale_algorithm_options() for details.
enpy_opts: options for the ENPY initial estimates, created with the enpy_options() function. See enpy_initial_estimates() for details.
cv_k, cv_objective: deprecated and ignored. See pense_cv() for estimating prediction performance via cross-validation.
...: ignored. See the section on deprecated parameters below.

Value

a list-like object with the following items

alpha

the sequence of alpha parameters.

lambda

a list of sequences of penalization levels, one per alpha parameter.

estimates

a list of estimates. Each estimate contains the following information:

intercept: intercept estimate.
beta: beta (slope) estimate.
lambda: penalization level at which the estimate is computed.
alpha: alpha hyper-parameter at which the estimate is computed.
bdp: chosen breakdown-point.
objf_value: value of the objective function at the solution.
statuscode: if > 0 the algorithm experienced issues when computing the estimate.
status: optional status message from the algorithm.

bdp

the actual breakdown point used.

call

the original call.

Strategies for Using Starting Points

The function supports several different strategies to compute, and use the provided starting points for optimizing the PENSE objective function.

Starting points are computed internally but can also be supplied via other_starts. By default, starting points are computed internally by the EN-PY procedure for penalization levels supplied in enpy_lambda (or the automatically generated grid of length nlambda_enpy). By default, starting points computed by the EN-PY procedure are shared for all penalization levels in lambda (or the automatically generated grid of length nlambda). If the starting points should be specific to the penalization level the starting points' penalization level, set the enpy_specific argument to TRUE.

In addition to EN-PY initial estimates, the algorithm can also use the "0-based" strategy if add_zero_based = TRUE (by default). Here, the 0-vector is used to start the optimization at the largest penalization level in lambda. At subsequent penalization levels, the solution at the previous penalization level is also used as starting point.

At every penalization level, all starting points are explored using the loose numerical tolerance explore_tol. Only the best explore_solutions are computed to the stringent numerical tolerance eps. Finally, only the best max_solutions are retained and carried forward as starting points for the subsequent penalization level.

Deprecated Arguments

Starting with version 2.0.0, cross-validation is performed by separate function pense_cv(). Arguments related cross-validation cause an error when supplied to pense(). Furthermore, the following arguments are deprecated as of version 2.0.0: initial, warm_reset, cl, options, init_options, en_options. If pense() is called with any of these arguments, warnings detail how to replace them.

Examples

# Compute the PENSE regularization path for Freeny's revenue data
# (see ?freeny)
data(freeny)
x <- as.matrix(freeny[ , 2:5])

regpath <- pense(x, freeny$y, alpha = 0.5)
plot(regpath)


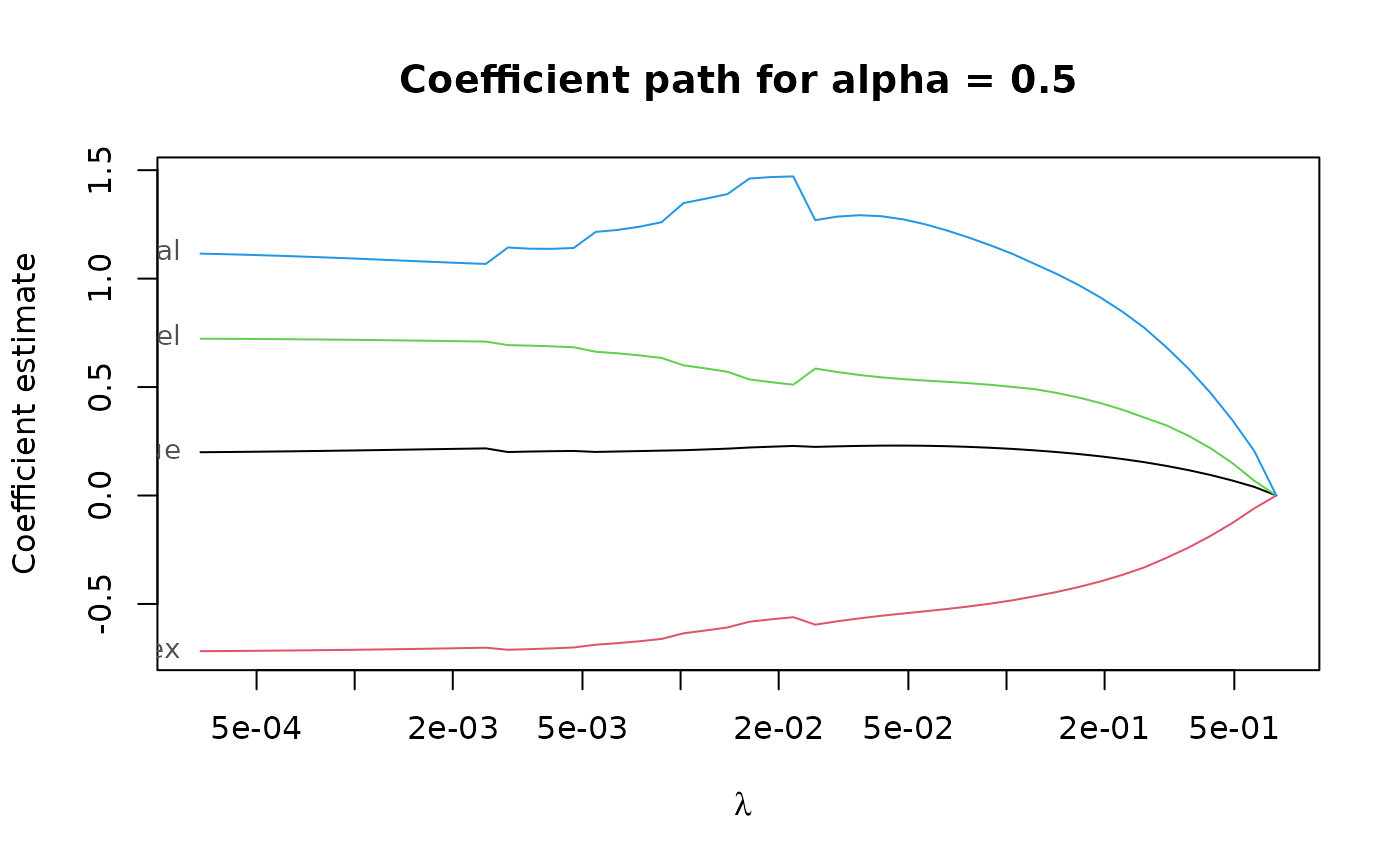# Extract the coefficients at a certain penalization level
coef(regpath, lambda = regpath$lambda[[1]][[40]])
#>           (Intercept) lag.quarterly.revenue           price.index 
#>           -23.9028248             0.1198500            -0.4955058 
#>          income.level      market.potential 
#>             0.4144162             2.4357470 

# What penalization level leads to good prediction performance?
set.seed(123)
cv_results <- pense_cv(x, freeny$y, alpha = 0.5,
                       cv_repl = 2, cv_k = 4)
plot(cv_results, se_mult = 1)


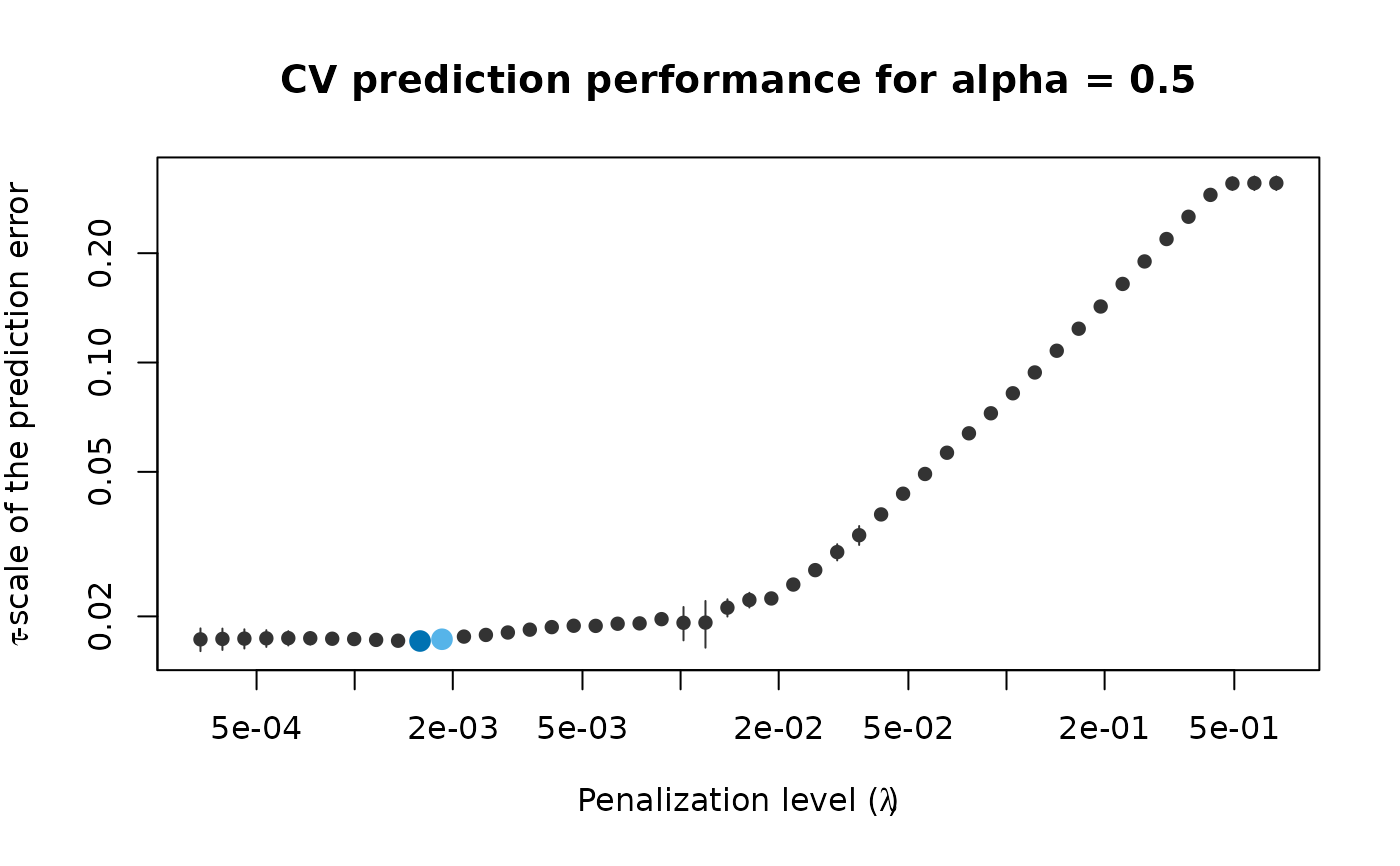# Print a summary of the fit and the cross-validation results.
summary(cv_results)
#> PENSE fit with prediction performance estimated by 2 replications of 4-fold ris 
#> cross-validation.
#> 
#> 4 out of 4 predictors have non-zero coefficients:
#> 
#>                Estimate
#> (Intercept) -16.3437416
#> X1            0.1769018
#> X2           -0.5800804
#> X3            0.5152704
#> X4            1.7991073
#> ---
#> 
#> Hyper-parameters: lambda=0.004700238, alpha=0.5

# Extract the coefficients at the penalization level with
# smallest prediction error ...
coef(cv_results)
#>           (Intercept) lag.quarterly.revenue           price.index 
#>           -16.3437416             0.1769018            -0.5800804 
#>          income.level      market.potential 
#>             0.5152704             1.7991073 
# ... or at the penalization level with prediction error
# statistically indistinguishable from the minimum.
coef(cv_results, lambda = '1-se')
#>           (Intercept) lag.quarterly.revenue           price.index 
#>            -5.0900585             0.1807610            -0.3989357 
#>          income.level      market.potential 
#>             0.4192179             0.9172138