Compute least squares EN estimates for linear regression with optional observation weights and penalty loadings.
elnet(
x,
y,
alpha,
nlambda = 100,
lambda_min_ratio,
lambda,
penalty_loadings,
weights,
intercept = TRUE,
en_algorithm_opts,
sparse = FALSE,
eps = 1e-06,
standardize = TRUE,
correction = deprecated(),
xtest = deprecated(),
options = deprecated()
)Arguments
- x
nbypmatrix of numeric predictors.- y
vector of response values of length
n. For binary classification,yshould be a factor with 2 levels.- alpha
elastic net penalty mixing parameter with \(0 \le \alpha \le 1\).
alpha = 1is the LASSO penalty, andalpha = 0the Ridge penalty. Can be a vector of several values, butalpha = 0cannot be mixed with other values.- nlambda
number of penalization levels.
- lambda_min_ratio
Smallest value of the penalization level as a fraction of the largest level (i.e., the smallest value for which all coefficients are zero). The default depends on the sample size relative to the number of variables and
alpha. If more observations than variables are available, the default is1e-3 * alpha, otherwise1e-2 * alpha.- lambda
optional user-supplied sequence of penalization levels. If given and not
NULL,nlambdaandlambda_min_ratioare ignored.- penalty_loadings
a vector of positive penalty loadings (a.k.a. weights) for different penalization of each coefficient.
- weights
a vector of positive observation weights.
- intercept
include an intercept in the model.
- en_algorithm_opts
options for the EN algorithm. See en_algorithm_options for details.
- sparse
use sparse coefficient vectors.
- eps
numerical tolerance.
- standardize
standardize variables to have unit variance. Coefficients are always returned in original scale.
- correction
defunct. Correction for EN estimates is not supported anymore.
- xtest
defunct.
- options
deprecated. Use
en_algorithm_optsinstead.
Value
a list-like object with the following items
alphathe sequence of
alphaparameters.lambdaa list of sequences of penalization levels, one per
alphaparameter.estimatesa list of estimates. Each estimate contains the following information:
interceptintercept estimate.
betabeta (slope) estimate.
lambdapenalization level at which the estimate is computed.
alphaalpha hyper-parameter at which the estimate is computed.
statuscodeif
> 0the algorithm experienced issues when computing the estimate.statusoptional status message from the algorithm.
callthe original call.
Details
The elastic net estimator for the linear regression model solves the optimization problem
$$argmin_{\mu, \beta} (1/2n) \sum_i w_i (y_i - \mu - x_i' \beta)^2 + \lambda \sum_j 0.5 (1 - \alpha) \beta_j^2 + \alpha l_j |\beta_j| $$
with observation weights \(w_i\) and penalty loadings \(l_j\).
See also
pense() for an S-estimate of regression with elastic net penalty.
coef.pense_fit() for extracting coefficient estimates.
plot.pense_fit() for plotting the regularization path.
Other functions for computing non-robust estimates:
elnet_cv()
Examples
# Compute the LS-EN regularization path for Freeny's revenue data
# (see ?freeny)
data(freeny)
x <- as.matrix(freeny[ , 2:5])
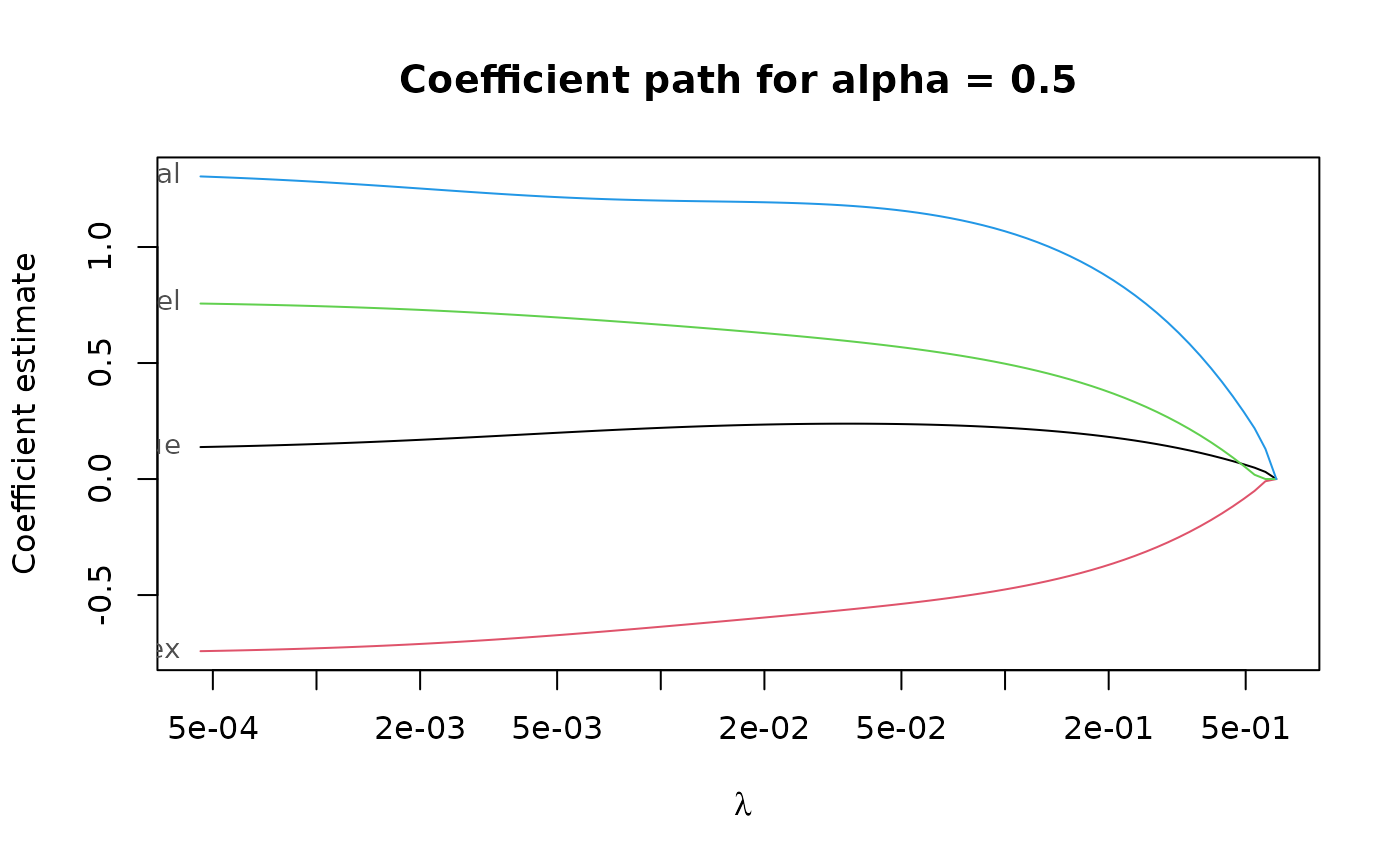
regpath <- elnet(x, freeny$y, alpha = c(0.5, 0.75))
plot(regpath)
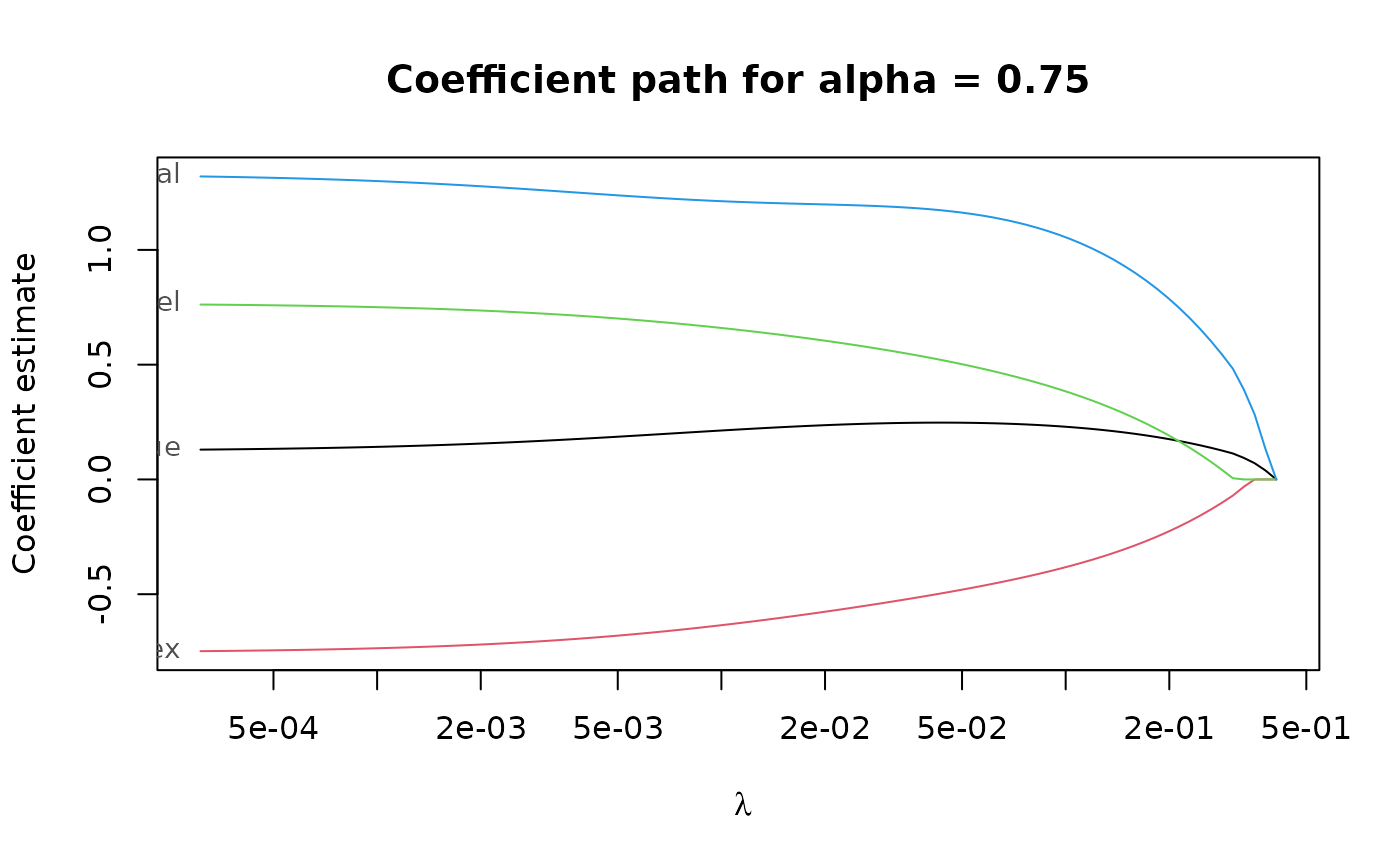
 plot(regpath, alpha = 0.75)
plot(regpath, alpha = 0.75)
 # Extract the coefficients at a certain penalization level
coef(regpath, lambda = regpath$lambda[[1]][[5]],
alpha = 0.75)
#> (Intercept) lag.quarterly.revenue price.index
#> 9.306304 0.000000 0.000000
#> income.level market.potential
#> 0.000000 0.000000
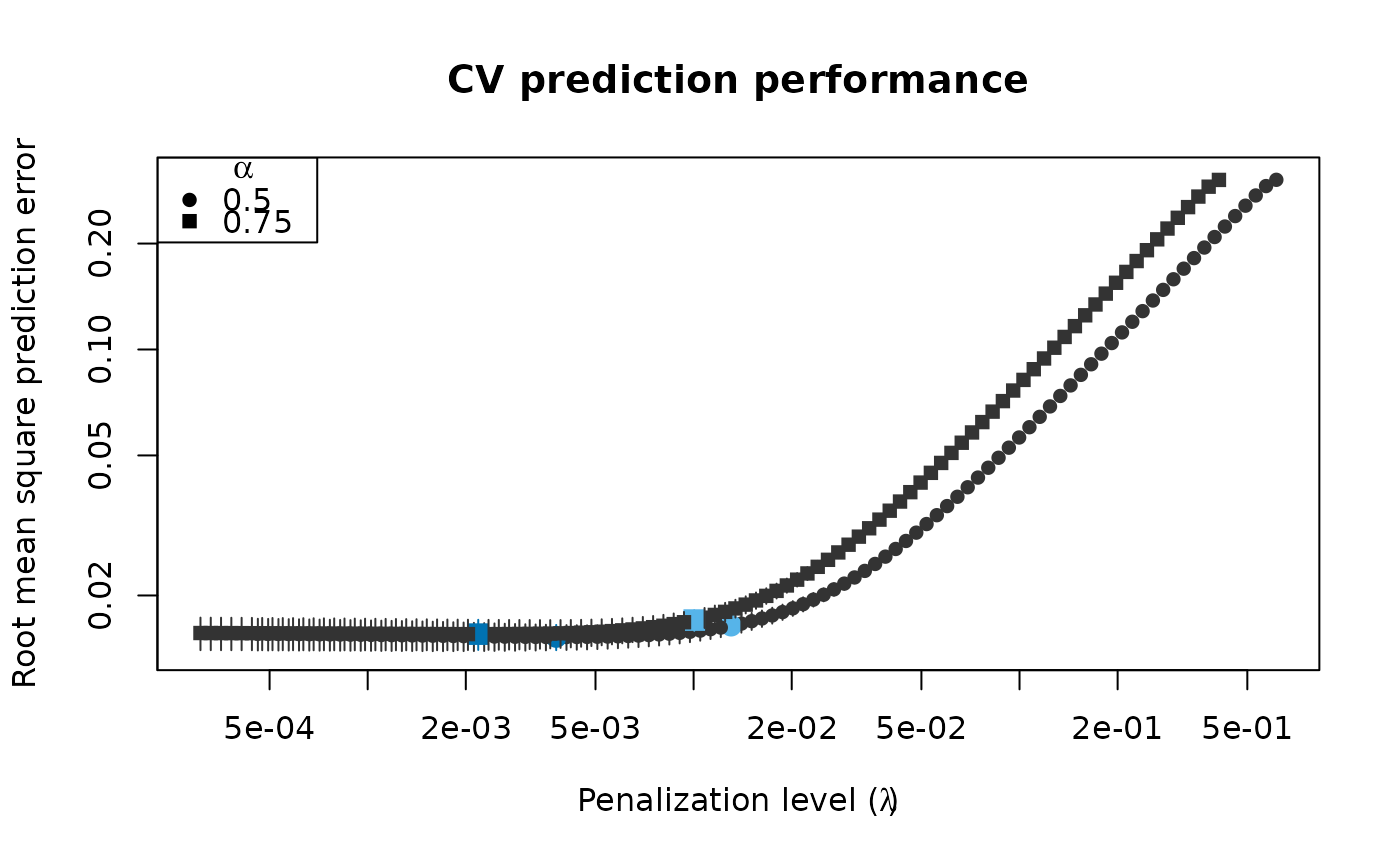
# What penalization level leads to good prediction performance?
set.seed(123)
cv_results <- elnet_cv(x, freeny$y, alpha = c(0.5, 0.75),
cv_repl = 10, cv_k = 4,
cv_measure = "tau")
plot(cv_results, se_mult = 1.5)
# Extract the coefficients at a certain penalization level
coef(regpath, lambda = regpath$lambda[[1]][[5]],
alpha = 0.75)
#> (Intercept) lag.quarterly.revenue price.index
#> 9.306304 0.000000 0.000000
#> income.level market.potential
#> 0.000000 0.000000
# What penalization level leads to good prediction performance?
set.seed(123)
cv_results <- elnet_cv(x, freeny$y, alpha = c(0.5, 0.75),
cv_repl = 10, cv_k = 4,
cv_measure = "tau")
plot(cv_results, se_mult = 1.5)
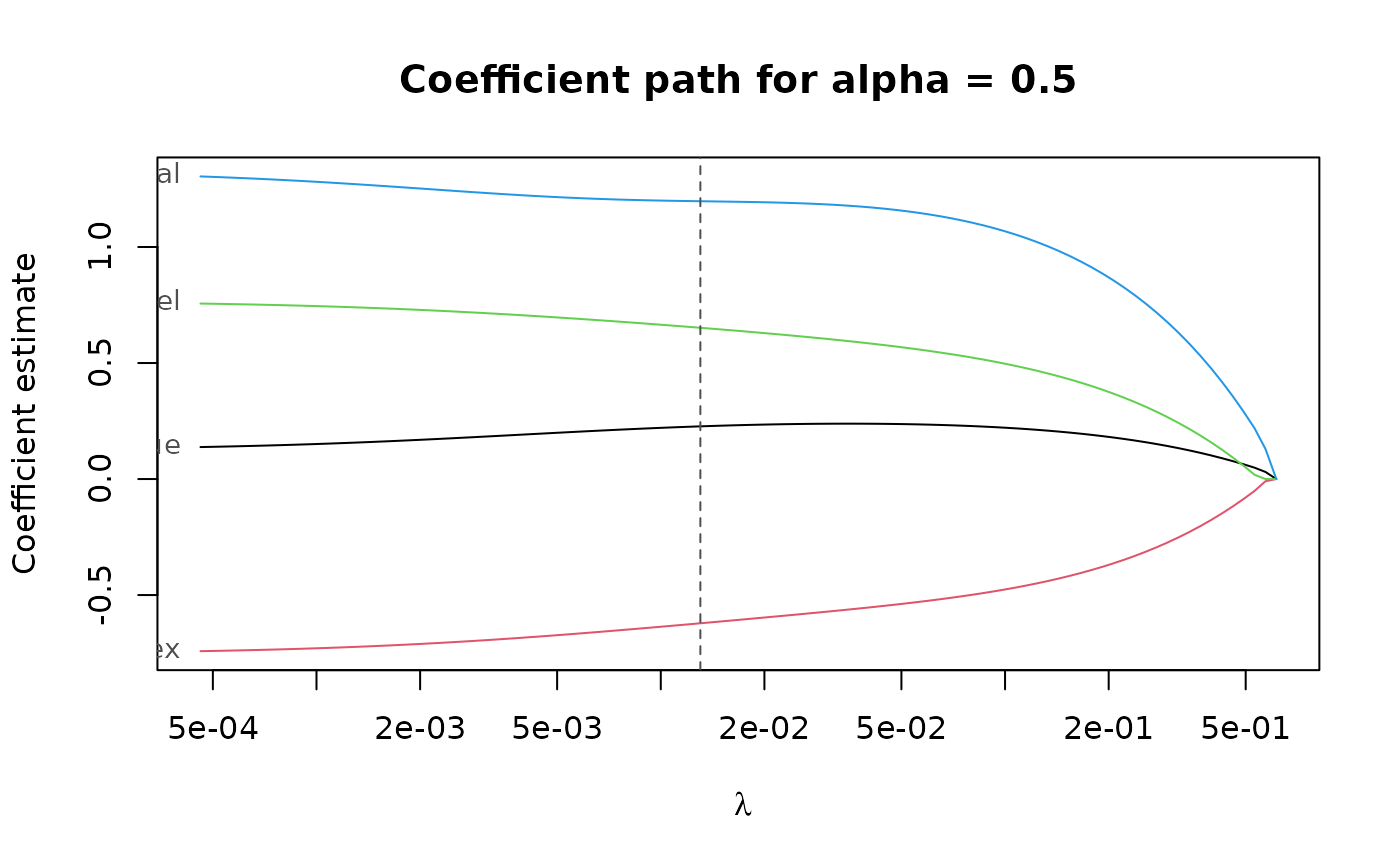
 plot(cv_results, se_mult = 1.5, what = "coef.path")
plot(cv_results, se_mult = 1.5, what = "coef.path")
 # Extract the coefficients at the penalization level with
# smallest prediction error ...
summary(cv_results)
#> EN fit with prediction performance estimated by replications of 4-fold
#> cross-validation.
#>
#> 4 out of 4 predictors have non-zero coefficients:
#>
#> Estimate
#> (Intercept) -9.6491805
#> X1 0.1899399
#> X2 -0.6858733
#> X3 0.7075924
#> X4 1.2247539
#> ---
#>
#> Hyper-parameters: lambda=0.003787891, alpha=0.5
coef(cv_results)
#> (Intercept) lag.quarterly.revenue price.index
#> -9.6491805 0.1899399 -0.6858733
#> income.level market.potential
#> 0.7075924 1.2247539
# ... or at the penalization level with prediction error
# statistically indistinguishable from the minimum.
summary(cv_results, lambda = "1.5-se")
#> EN fit with prediction performance estimated by replications of 4-fold
#> cross-validation.
#>
#> 4 out of 4 predictors have non-zero coefficients:
#>
#> Estimate
#> (Intercept) -9.5875726
#> X1 0.2270959
#> X2 -0.6216322
#> X3 0.6519060
#> X4 1.1972788
#> ---
#>
#> Hyper-parameters: lambda=0.01303176, alpha=0.5
coef(cv_results, lambda = "1.5-se")
#> (Intercept) lag.quarterly.revenue price.index
#> -9.5875726 0.2270959 -0.6216322
#> income.level market.potential
#> 0.6519060 1.1972788
# Extract the coefficients at the penalization level with
# smallest prediction error ...
summary(cv_results)
#> EN fit with prediction performance estimated by replications of 4-fold
#> cross-validation.
#>
#> 4 out of 4 predictors have non-zero coefficients:
#>
#> Estimate
#> (Intercept) -9.6491805
#> X1 0.1899399
#> X2 -0.6858733
#> X3 0.7075924
#> X4 1.2247539
#> ---
#>
#> Hyper-parameters: lambda=0.003787891, alpha=0.5
coef(cv_results)
#> (Intercept) lag.quarterly.revenue price.index
#> -9.6491805 0.1899399 -0.6858733
#> income.level market.potential
#> 0.7075924 1.2247539
# ... or at the penalization level with prediction error
# statistically indistinguishable from the minimum.
summary(cv_results, lambda = "1.5-se")
#> EN fit with prediction performance estimated by replications of 4-fold
#> cross-validation.
#>
#> 4 out of 4 predictors have non-zero coefficients:
#>
#> Estimate
#> (Intercept) -9.5875726
#> X1 0.2270959
#> X2 -0.6216322
#> X3 0.6519060
#> X4 1.1972788
#> ---
#>
#> Hyper-parameters: lambda=0.01303176, alpha=0.5
coef(cv_results, lambda = "1.5-se")
#> (Intercept) lag.quarterly.revenue price.index
#> -9.5875726 0.2270959 -0.6216322
#> income.level market.potential
#> 0.6519060 1.1972788